[新しいコレクション] gravitational potential energy formula with angle 313282-How to gravitational potential energy
Formula Gravitational Potential Energy = Mass (kg)x Gravitational Acceleration x Height(m) Where, Gravitational Acceleration = 98 m/s 21) Gravitational potential energy (J) = work done to move a mass from one place to another through a gravitational field (use mgΔh or GMm(1/R11/R2) 2) Gravitational potential (Jkg1) = work done per unit mass to move a small object from infinity to that point (V=W/m)To define quantitatively what we mean by the strength of a gravitational field, which is merely the force experienced by unit mass placed in the field I shall use the symbol g for the gravitational field, so that the force F on a mass m situated in a gravitational field g is F = mg 521 It can be expressed in newtons per kilogram, N kg1
Physicslab Gravitational Potential Energy
How to gravitational potential energy
How to gravitational potential energy-Gravitational potential energy can be calculated by using the gravitational potential energy formula when you know the mass and height of the object in question where the angleFormula work, potential, kinetic are at an angle, θ , to each other) of gravitational potential energy and kinetic energy) in an isolated system remains constant A system is isolated when the net external force (excluding the gravitational force) acting on
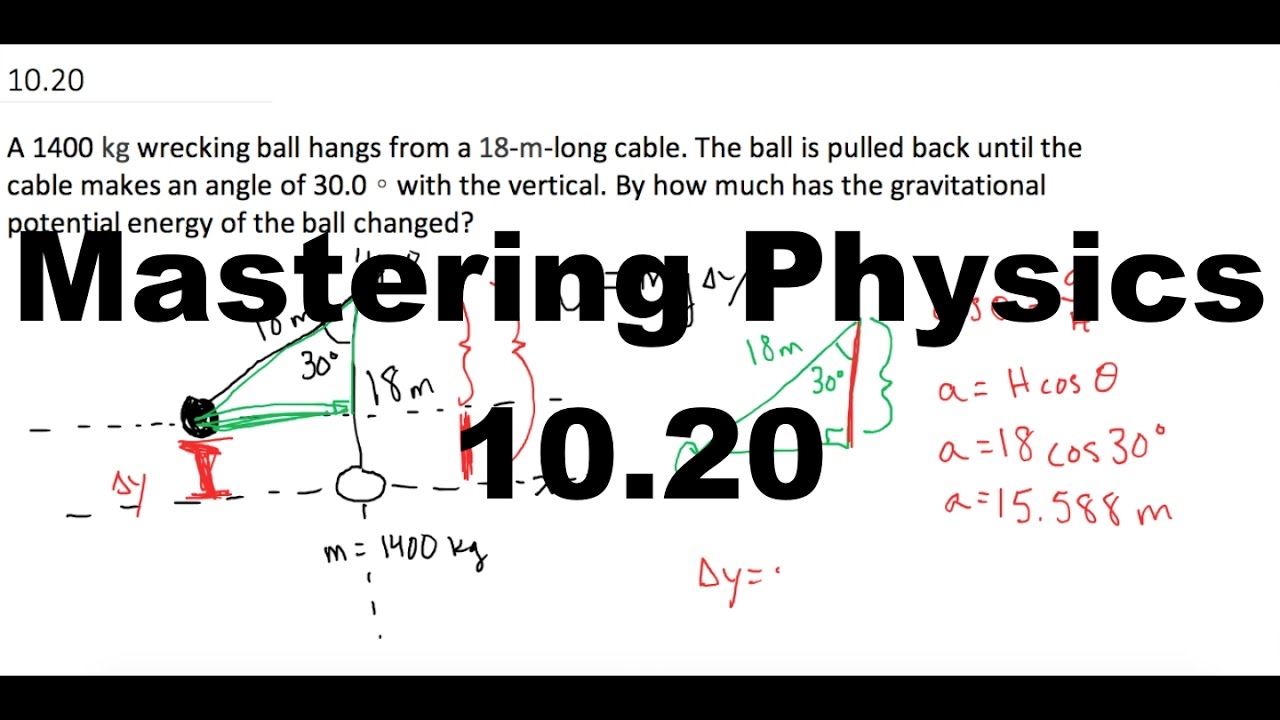



Mastering Physics 10 A 1400 Kg Wrecking Ball Hangs From A 18 M Long Cable The Ball Is Pulled Youtube
· In this equation, and Gravitational potential energy Gravitational potential energy or GPE is a type of potential energy possessed by an object due to its position in a gravitational field (Hyperphysicsphyastrgsuedu, 17) One way to demonstrate this concept is a ball rolling down an inclineGravitational field intensity = 98 Nkg 1 Gravitational potential energy gained = mg D h = 300x98x25 = 7350 J 2 A mass of 25 kg is moved a distance of 35 m at an angle of o to a gravitational field of intensity 98 Nkg 1 Calculate the change in gravitational energy Change in gravitational potential energy = 25x98x35cos = 8057 JThe gravitational potential energy, U U, of a system of masses m1 m 1 and M2 M 2 at a distance r r using gravitational constant G G is U= −Gm1M2 r U = − G m 1 M 2 r
The change in gravitational potential energy, ΔPE g, is ΔPE g = mgh, with h being the increase in height and g the acceleration due to gravity The gravitational potential energy of an object near Earth's surface is due to its position in the massEarth systemThe flight path angle (φ) is the angle between the direction of velocity and the perpendicular to the radial direction, so it is zero at periapsis and tends to 90 degrees at infinityRecall that the gravitational potential per unit mass is given by −µ/r That 2is, F /m = − (−µ/r) = −(µ/r )e r Note that the origin (zero potential) for the gravitational potential is taken to be at infinity Therefore, for finite values of r, the potential is negative The kinetic energy per unit mass is v2/2 Therefore, 1 v 2 µ
The work done by gravity can be calculated with the formula, where F is the gravitational force, Δr is the total displacement and θ is the angle between the force and the displacementThose with zero or greater are unboundedGravitational Potential Energy Formula The formula for gravitational potential energy is the following U = – G*M*m/r Where U is the potential energy;



2



Practical Report Bounce Efficiency
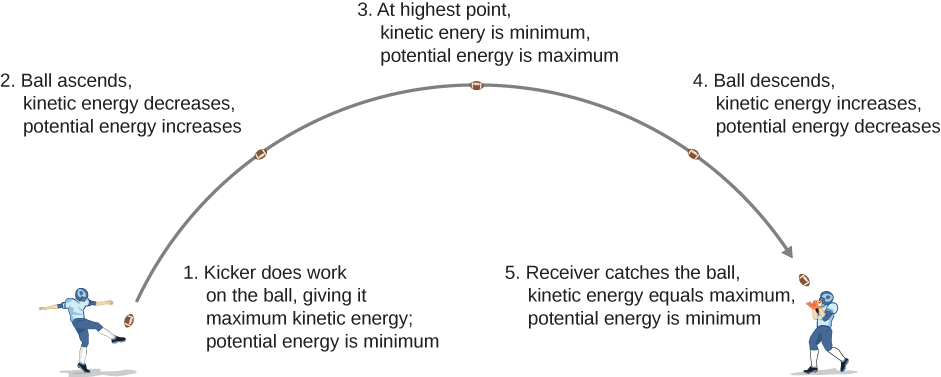
· At time 2, the gravitational potential energy equals the kinetic energy At the bottom of its path (time 3), the GPE tank has totally emptied into the KE tank, and the mass is at its maximum velocityAs the resistive force to motion is due to gravity, we are talking about gravitational potential energy We need to use the formula U = mgh Plugging in the values that are provided, we can solve for the potential energy (U) U = (2kg)(98m/s 2)(5m) = 98J The amount of work required is equal to the change in potential energy of the platformCalculate the unknown variable in the equation for gravitational potential energy, where potential energy is equal to mass multiplied by gravity and height;




Learn Ap Physics Ap Physics 1 2 Work And Energy




Conservation Of Energy In Projectile Motion Examples Analysis Video Lesson Transcript Study Com
Let's do a little bit of review of potential energy and especially gravitational potential energy because in this video we're going to get a little bit more precise so let's say that I have an object here it has a mass of m and I were to change its position in the vertical direction we're assuming that we are on earth where the gravitational field is G and we have a change in the vertical · The gravitational potential energy of this ball depends on two factors the mass of the ball and the height it's raised to The relationship between gravitational potential energy and the mass and height of an object is described by the following equation PE grav = m * h * gGravitational potential energy is usually given the symbol It represents the potential an object has to do work as a result of being located at a particular position in a gravitational field Consider an object of mass being lifted through a height against the force of gravity as shown below The object is lifted vertically by a pulley and



Physics Tutorial Electric Potential



8 1 Potential Energy Of A System University Physics Volume 1
In terms of potential energy, the equilibrium position could be called the zeropotential energy position There is a special equation for springs that relates the amount of elastic potential energy to the amount of stretch (or compression) and the spring constant The equation is PEspring = 05 • · The upward force required while moving at a constant velocity is equal to the weight, m g, of an object, so the work done in lifting it through a height h is the product m g h Thus, when accounting only for mass, gravity, and altitude, the equation is (571) U = m g h where U is the potential energy of the object relative to its being onBecause the horizontal portion is frictionless, the kinetic energy at the bottom of the second incline is the same as the kinetic energy at the bottom of the first That is (Ek)bottom 2 = (Ek)bottom 1 = ½ m v2 = ½ m (225 m2/s2) Now write the gravitational potential energy equation for the top and bottom of the second incline
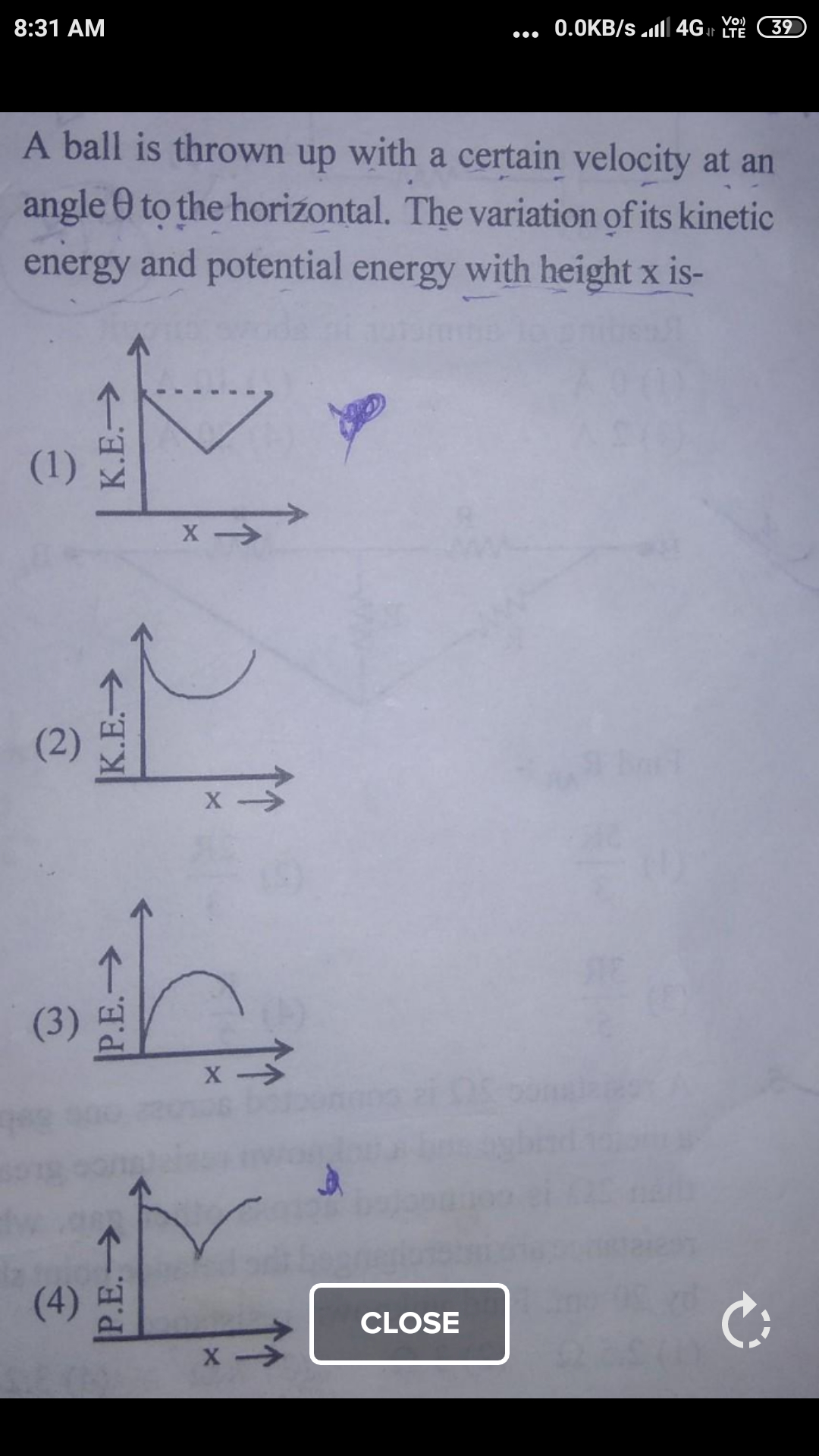



Find Relation Between Potential Energy And Kinetic Energy At Height X Graph Refer To Attachment Help Me In Thisthanks Ry Physics Topperlearning Com



Mostly About Potential Energy
Let us define the gravitational potential energy as Ω so that the gravitational force will be r (413) Now by analogy with the electromagnetic force, let us define the gravitational field G r as the gravitational force per unit mass so that r r G (414) Here Φ is known as the gravitational potential, and from the form of equationPROBLEM #2 USING POTENTIAL ENERGY Lab III 5 PROBLEM #2 USING POTENTIAL ENERGY Redo the calculations for one of the problems from Lab 2 problems 1 – 5 by redefining your system so that you can use potential energy Use the data you have already recorded in your lab journal to test your calculations Read Serway & Jewett sections 7173Here is the equation for calculating gravitational potential energy \GPE = mgh~~or~~GPE = m \times g \times h \ where GPE is the gravitational potential energy in joules, J




Subtle Concepts Of Work And Energy




Solved A Ball Is Thrown From The Top Of A Cliff At An Ang Chegg Com
In other words, Where W is the gravitational potential energy of the pendulum at an instant KE is the kinetic energy of the pendulum at an instant C is a constant The gravitational potential energy of the pendulum is where m is the mass of the rigid body, and Therefore, The kinetic energy of the pendulum is where I p is the moment of inertia of the pendulum about an axisThe energy is most commonly used for an object near the surface of the Earth where the gravitational acceleration can be assumed to be constant at about 98 m/s2 GPE changes into kinetic energy The gravitational potential energy formula is GPE = mgh, where m is the mass in kilograms, g is the acceleration due to gravity (98 on Earth), and h is the height above theF21 Gm1m2rˆ r2 and the gravitational potential energy is, V (r) = Zr ∞ F dr 0 = r Gm 1m 2 r 0 2) dr Gm m r (The prime (0) on the integration variable is simply to distinguish it from the point where we are evaluating the potential energy) It is also useful to think of particle 1 setting up a gravitational field which acts on particle 2




Energy In The Physical Pendulum Physics Stack Exchange




1 Gravitational Potential Near The Earth S Surface Chegg Com
· 406 15 potential energy only depends on the height, mgh whatever the difference in height at the start and end, mg (h2h1) will be the change in potential energy, either becoming kinetic (rolling down) or becoming potential (going up ramp) the potential has nothing to do with the ramp, only the change in height g never changes Share98 · fi~ = 2GMfl=c2Rfl = 0 arcsec for the de°ection angle of a light ray grazing the sun (here Mfl and Rfl are the mass and radius of the sun, c and G are the speed of light and the gravitational constant respectively) Einstein emphasized his wish that astronomers investigate this equation · For the WorkEnergy principle, a point mass can only have translational kinetic energy even though a system of the point mass and the Earth could also have gravitational potential energy




Q A Particle Is Projected At An Angle 8 30 With The Horizontal Which Of The Physics Kinematics Meritnation Com




Activity 1 3 Gravitational Potential Kinetic And Chegg Com
Universal gravitational constant, potential energy = velocity or speed W= work done on a system x = position = = = m coefficient of friction q = angle t = torque w angular speed a angular acceleration f = phase angle 2 q= angle CALCULUS df df duWhat had been mechanical tension in the spring became kinetic energy during the lift, and what had been kinetic energy is now gravitational potential energy in the mass sitting on the shelf The mass now has the energy equivalent mass increase —Supposed we have a large enough body to exert a gravitational force If so, we can define a gravitational potential proportional to 1/r, r the distance between the body and the object being bound If r = ∞, the binding potential is zero so as the




Gravitational Potential Energy Physics




Gravitational Potential Energy An Overview Sciencedirect Topics
The total energy of a system is the sum of kinetic and gravitational potential energy, and this total energy is conserved in orbital motion Objects must have a minimum velocity, the escape velocity, to leave a planet and not return Objects with total energy less than zero are bound;This formula can be used to calculate the energy gained when something is raised or the energy lost when an object falls m is the mass of the object, g is the acceleration due to gravity and h is the change in height The acceleration due to gravity (g) on the surface of the earth is 981 ms 2 This can usually be approximated to 10 ms 2 · The gravitational potential energy is given by U = GMm/r U = (6673 ∗ 1011 ∗ 598 ∗ 10 24 ∗199∗10 30)/(160∗10 9) = 4963 x 10 30 J Example 3 A basketball weighing 22 kg falls off a building to the ground 50 m below Calculate the gravitational potential energy of the ball when it arrives below Solution



Mostly About Potential Energy



Energy Basics
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsIn this video I derive a very commonly used formula in physics (GMm/r) that is often left unexplained by teachers in high school/sixth form classes DerivinPE = mgh Calculate GPE for different gravity of different enviornments Earth, the Moon, Jupiter, or specify your own Free online physics calculators, mechanics, energy, calculators




Gravitational Potential Energy At Large Distances Video Khan Academy




Pendulums In Physics Energy Exchange Calculations Video Lesson Transcript Study Com
PhysicsLAB Gravitational Potential Energy Recall that work is calculated with the formula W = Fs cos θ where θ is the angle between the direction of the force and the direction of the object's motion The work energy theorem states that the work done on an object equals the change in its kinetic energy, W = ΔKEG is the gravitational constant, M is mass 1, m is mass 2, and r is the radius between the two objects When looking at the potential energy of an object on earth, this can be simplified into the following U= m * g * hThe gravitational potential is negative due to the always attractive gravitational force, hence there is work done by the test mass, decreasing its potential gpe the work done in bringing an object from infinity to the point For a body of mass m, then the gravitational potential energy of the body will be m times




Section 2




Pin By Ncert Solutions On Cbse Tuts Physics Gravitational Potential Energy Linear Momentum
· Homework Statement A 023kg pendulum bob is attached to a string 12 long at an angle of 30 degrees What is the change in the gravitational potential energy of the system as the bob swings from point A to point B U= Homework Equations 5 mv^2 =
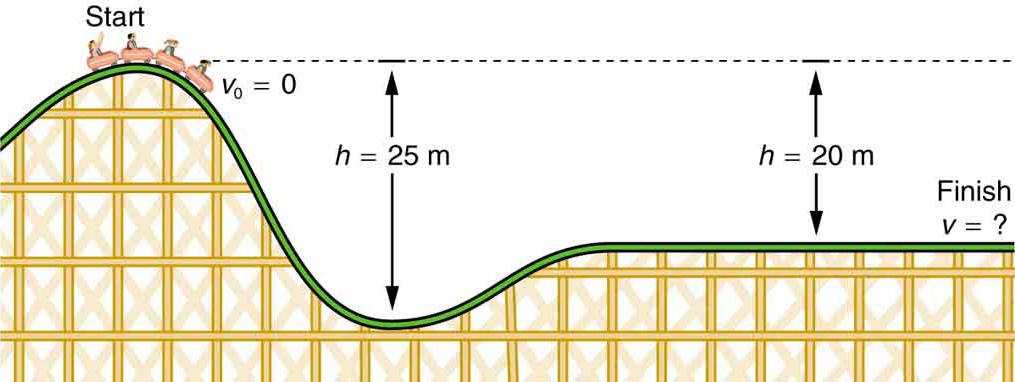



Gravitational Potential Energy Physics




Wep 1 Mass Kinetic Energy




Work And Electric Potential Energy Howtomechatronics




Gravitational Potential Energy Part 3 Calculating Height Youtube



Gravitational Potential Energy



New Page 1




What Is Gravitational Potential Energy Article Khan Academy




Mastering Physics 10 A 1400 Kg Wrecking Ball Hangs From A 18 M Long Cable The Ball Is Pulled Youtube




A Boy With A Mass Of 50 Kg Sits On A Swing Suspended By A Rope 5m Long A Person Pulls The Rope That Makes An Angle Of 30 Degrees With The



At Which Point Of Projectile Motion Is Kinetic Energy A Minimum And What Is Its Minimum Value Quora



1
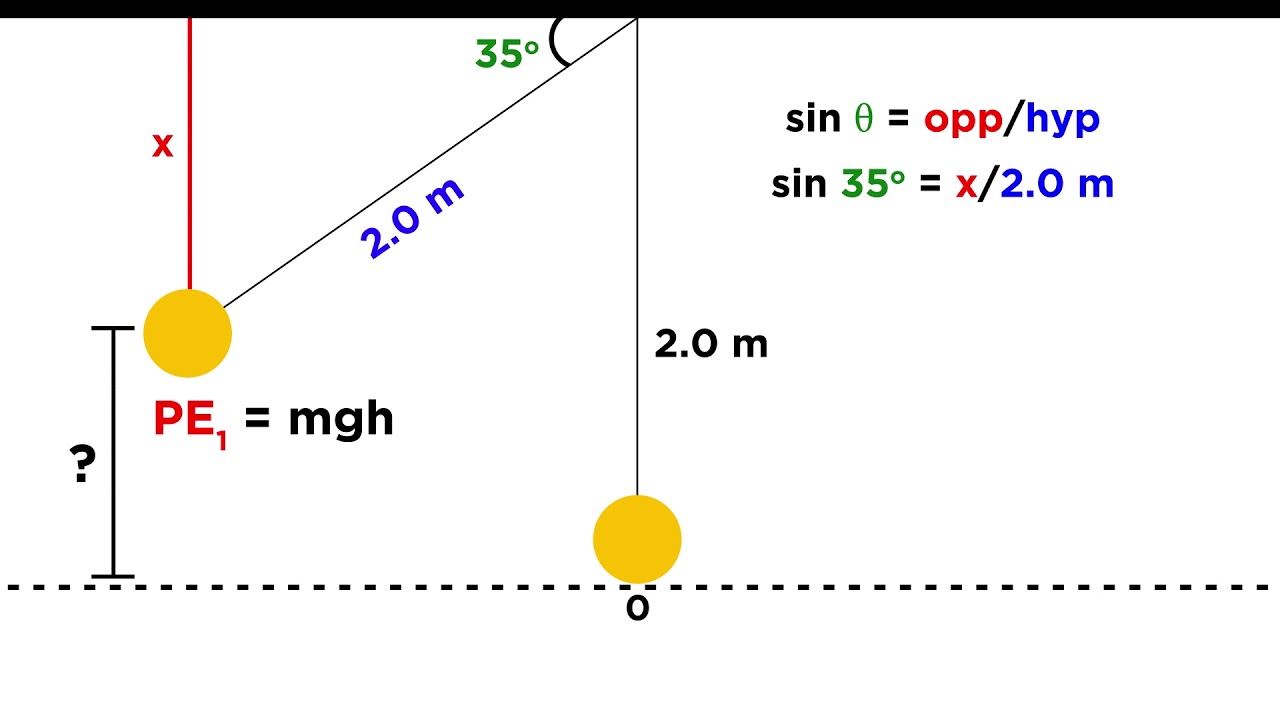



Practice Problem Pendulum Velocity Youtube



1



Physicslab Gravitational Potential Energy



Physicslab Gravitational Potential Energy




Conservation Of Energy In Projectile Motion Examples Analysis Video Lesson Transcript Study Com



Physicslab Gravitational Potential Energy



Energy In A Pendulum Gary Garber S Blog




Why Is The Work Done In Moving A Unit Mass From Infinity To A Point Where Gravitational Field Exists Negative Physics Stack Exchange




Potential Energy And Conservation Of Energy Ppt Download




Work And Electric Potential Energy Howtomechatronics



1



What S The Difference Between Work And Potential Energy Wired




Lesson Video Gravitational Potential Energy Nagwa



Gravitational Potential Energy




Solved The Gravitational Potential Energy Can Be Found Fr Chegg Com



2




Work Energy Problem With Friction Video Khan Academy



Potential Energy



What Is K E Of A Projectile At Its Maximum Height Quora




Gravitational Potential Energy Conservation Of Energy Ppt Video Online Download




Pendulums In Physics Energy Exchange Calculations Video Lesson Transcript Study Com



Gravitational Potential Energy




9 2 1define Gravitational Potential And Gravitational Potential Energy Understand That The Work Done In A Gravitational Field Is Independent Of Path Ppt Download




What S The Difference Between Work And Potential Energy Wired



Physicslab Gravitational Potential Energy




Calculating Rotational Kinetic Energy On A Ramp Dummies



Majeczkashutterstock Mechanical Energy Power Gravitational Potential Energy College



Ballistic Pendulum




Work And Energychapter Questions Docsbay
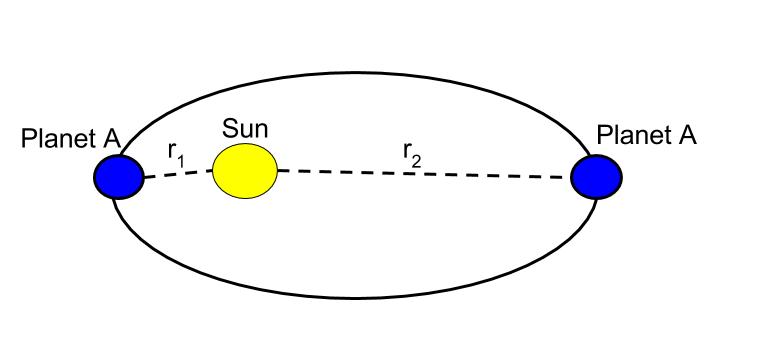



Gravitational Potential Energy At Large Distances Review Article Khan Academy
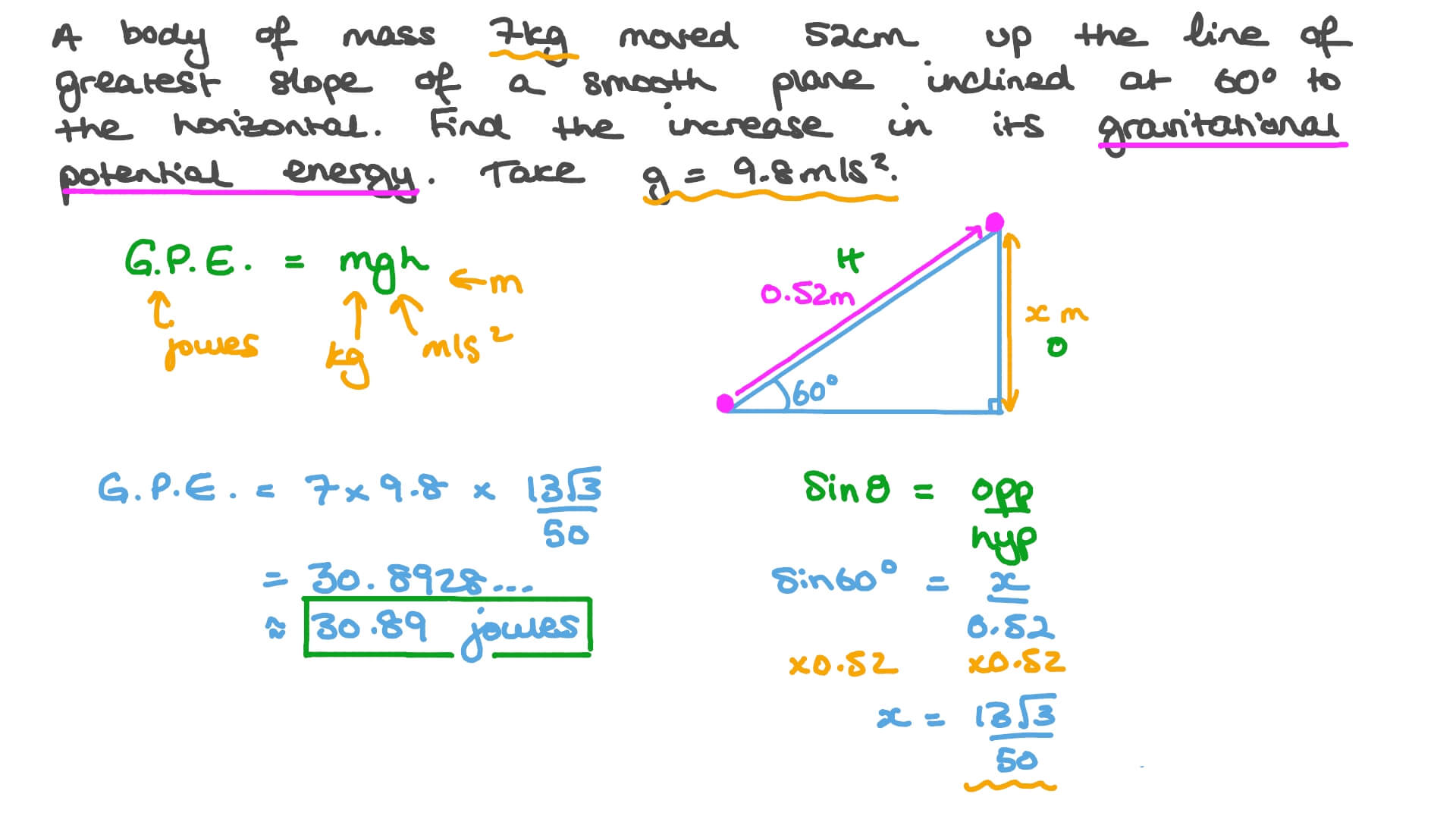



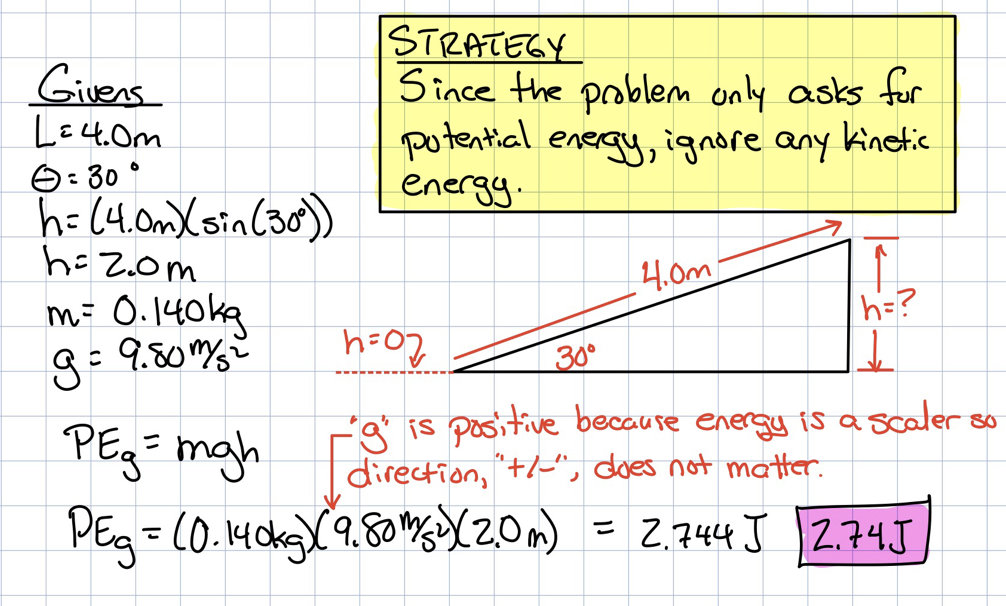
Question Video Finding The Increase In The Gravitational Potential Energy Of A Body Moving Up An Inclined Plane Nagwa



F00 Notes 12



31 A 0 60 Kg Basketball Is Dropped Out Of A Window That Is 6 1 M Above The Ground The Ball Is Caught By A Person Whose Hands Are 1 5 M Above The Ground A How Much Work Is Done On The Ball By Its Weight What Is The Gravitational Potential Energy Of



29 A 75 0 Kg Skier Rides A M Long Lift To The Top Of A Mountain The Lift Makes An Angle Of 14 6 With The Horizontal What Is The Change In The Skier S Gravitational Potential Energy Change In The Skier S Gravitational Potential Energy Is Found By We Know




Gravitational Potential Wikipedia
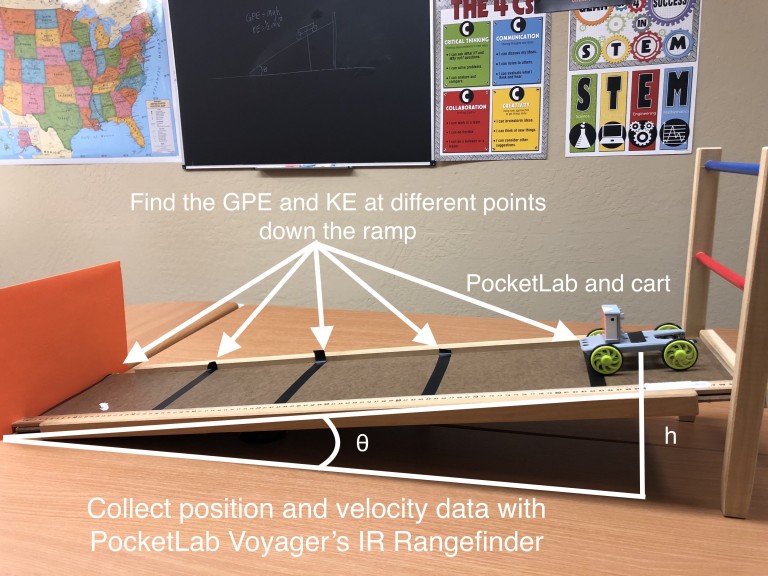



Potential Energy To Kinetic Energy Experiment Gravity Pocketlab




Gravitational Potential Energy Conservation Of Energy Ppt Video Online Download



The Physic Of Everyday Stuff Swings




Mastering Physics Solutions Chapter 8 Potential Energy And Conservation Of Energy A Plus Topper
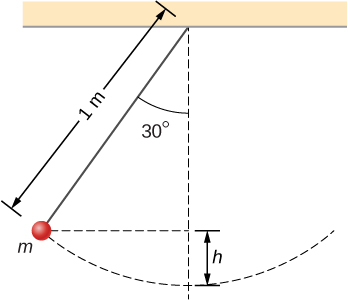



8 3 Conservation Of Energy University Physics Volume 1
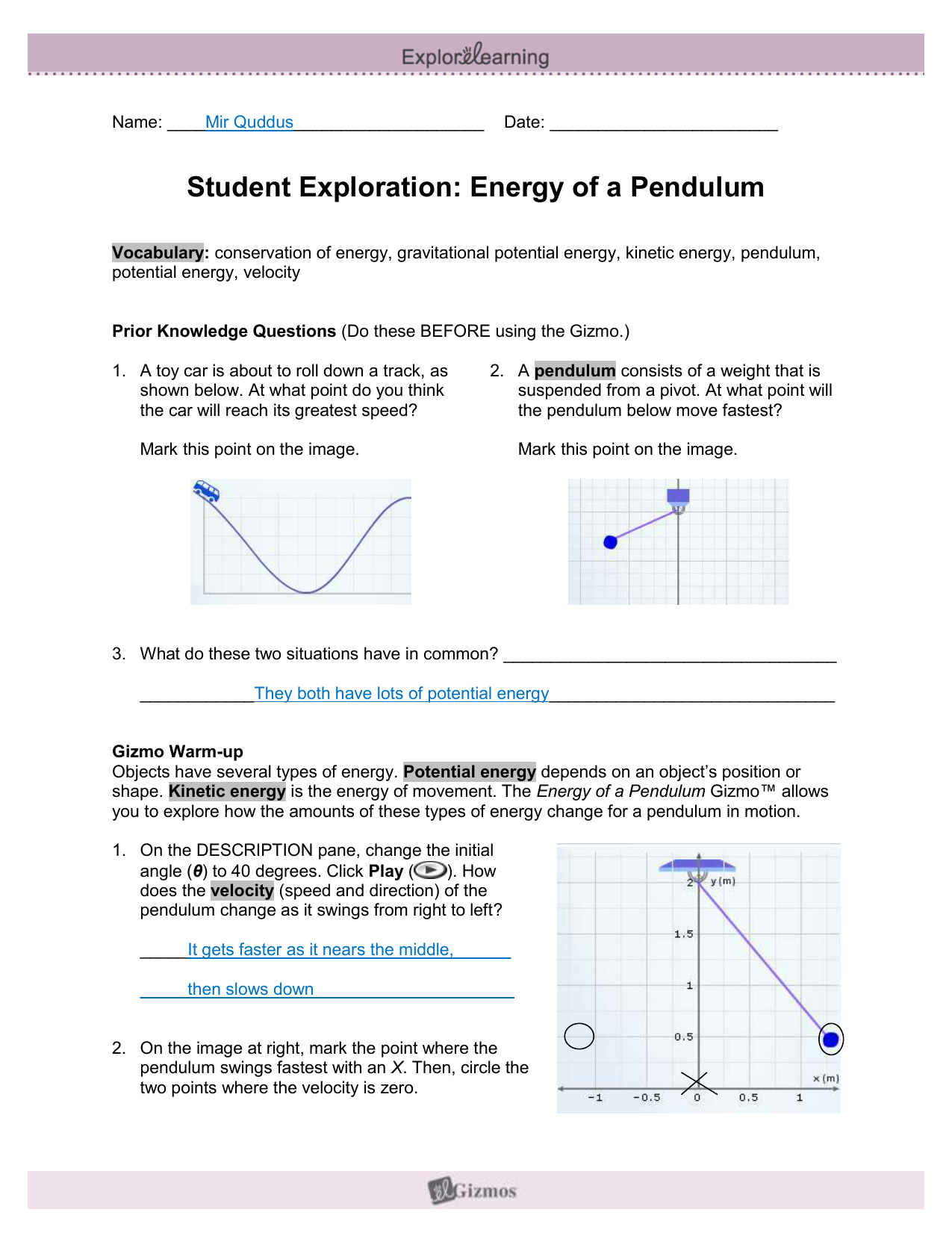



Modulesixlessonthreeactivityonegizmo
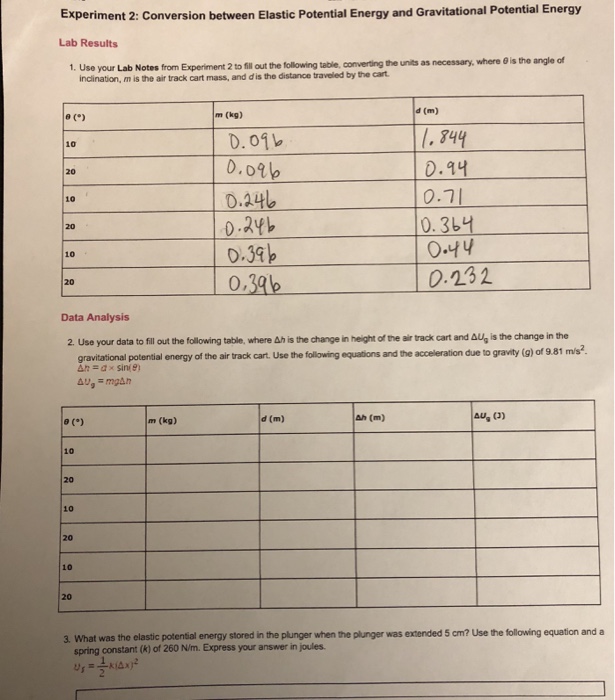



Experiment 2 Conversion Between Elastic Potential Chegg Com




Gravitational Potential Energy In A Pendulum Ld Industries Physics Youtube
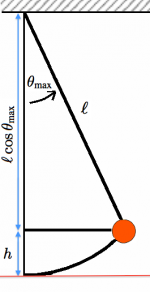



Physics Simple Harmonic Motion
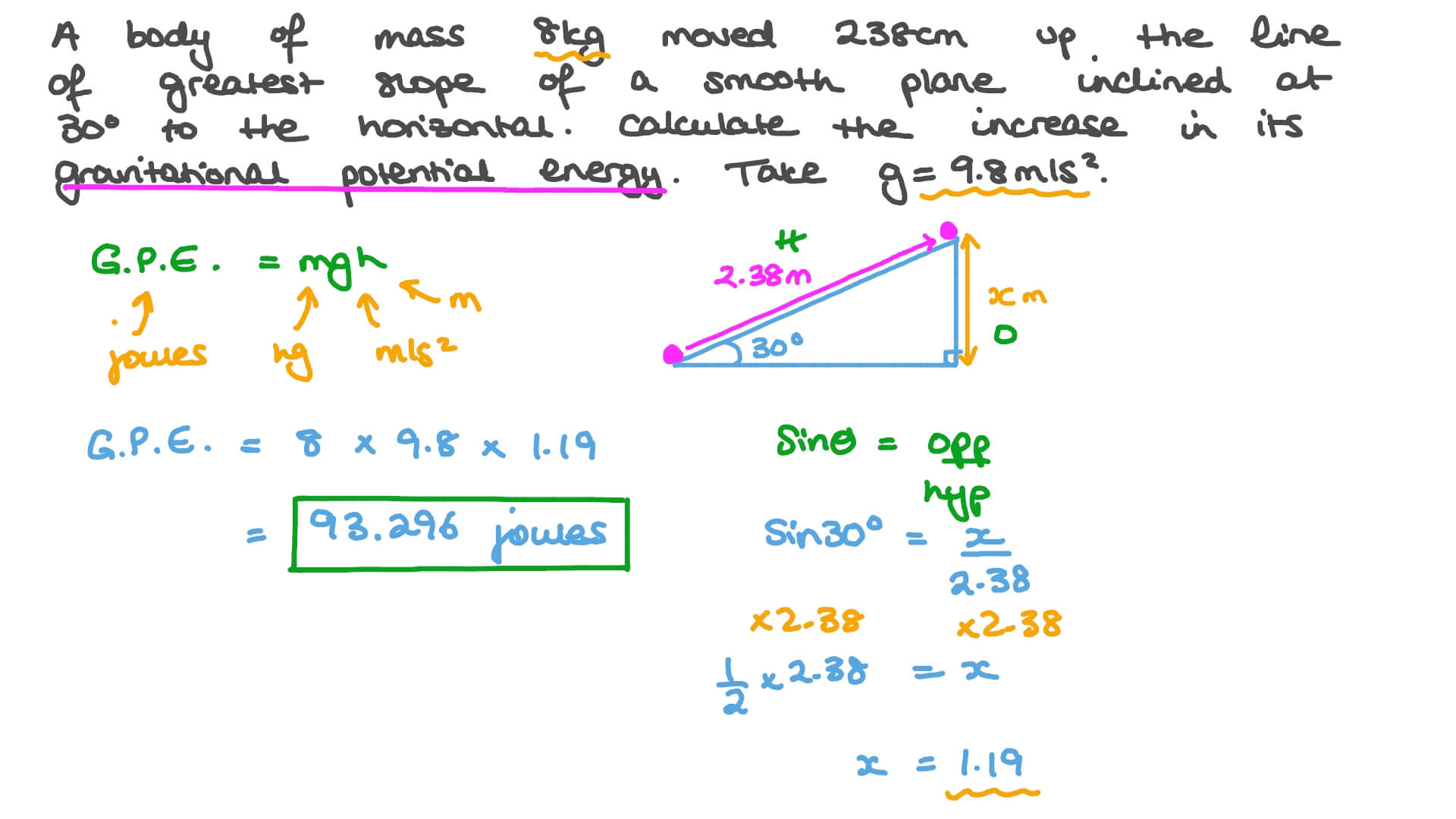



Question Video Finding The Increase In The Gravitational Potential Energy Of A Body Moving Up An Inclined Plane Nagwa
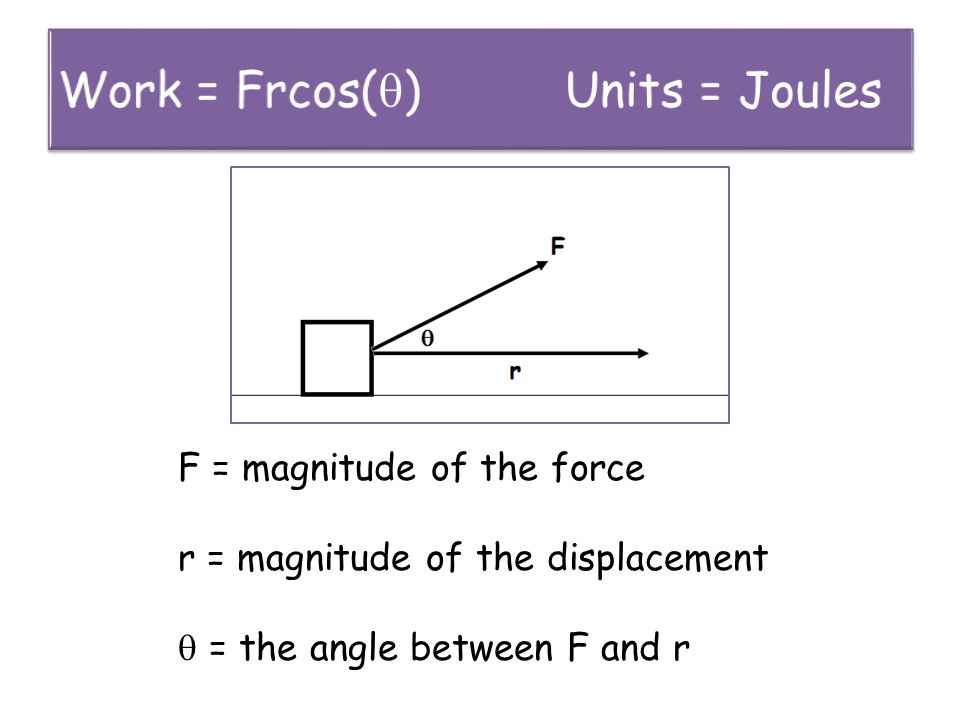



Work Kinetic Energy Work Energy Theorem Gravitational Potential Energy Mechanical Energy Conservation Of Energy Work Kinetic Energy Work Energy Theorem Ppt Download



Chapter 6




Why Is The Work Done In Moving A Unit Mass From Infinity To A Point Where Gravitational Field Exists Negative Physics Stack Exchange




Solved Vii Gravitational Potential Energy M Vib M2v2bm Chegg Com




Pin On Phy131 Week 7 Summary



What Is The Angle Of A Projection For Which The Kinetic Energy At The Highest Point Of Its Trajectory Is Equal To One Fourth Of Its Kinetic Energy At The Point Of




Mastering Physics Solutions Chapter 8 Potential Energy And Conservation Of Energy A Plus Topper



Gravitational Potential Energy Definition Formula Examples Video Lesson Transcript Study Com




Calculate Potential Energy Solution Youtube
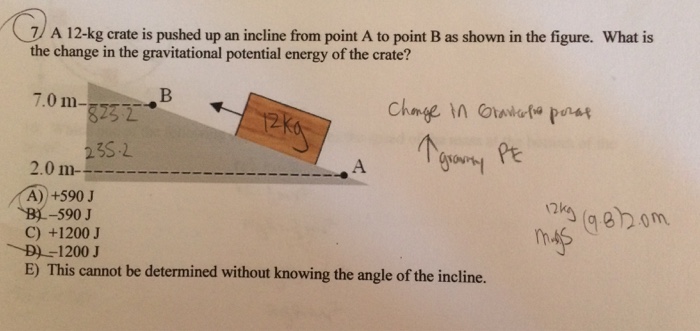



A 12 Kg Crate Is Pushed Up An Incline From Point A To Chegg Com




Potential Energy Ck 12 Foundation



1
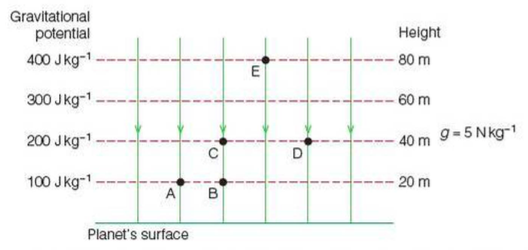



Gravitational Potential Digestible Notes




Rotational Kinetic Energy And Moment Of Inertia Examples Physics Problems Youtube



Unit 4 Work And Energy Physics Project




Lesson Playlist Nagwa




Chapter 5 Work And Energy Ppt Download



Http Aias Ae Wp Content Uploads 18 03 Grade 9 Answer Key Physicds 2nd Term Revision Sheets 17 18 Pdf
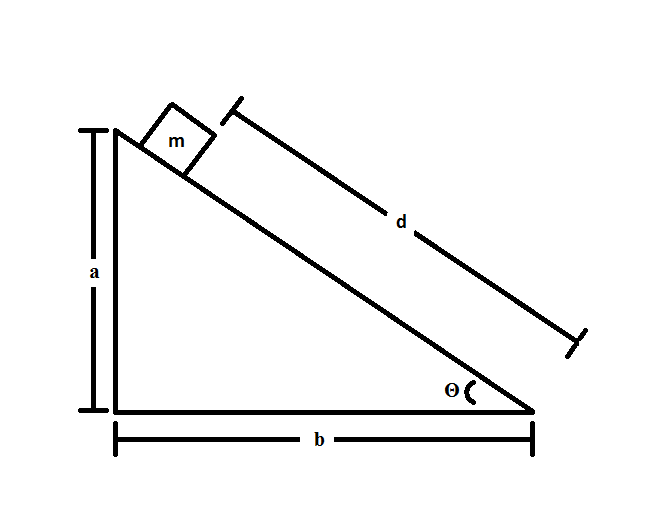



Gravitational Potential Energy Ap Physics 1



Formula For Gravitational Potential Energy With Solved Examples Physics Formulas



Potential Energy




Conservation Of Energy In Projectile Motion Examples Analysis Video Lesson Transcript Study Com



Sphere On Incline



Physicslab Gravitational Potential Energy



New Page 1
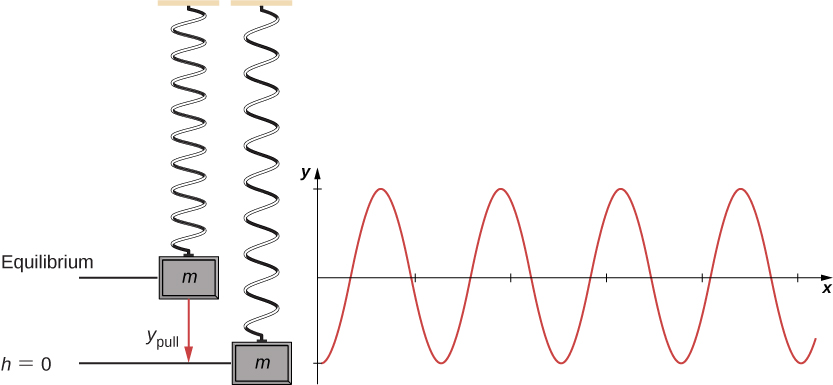



8 1 Potential Energy Of A System University Physics Volume 1


コメント
コメントを投稿