[10000印刷√] 1/cos^2x 微分 263188-1+cos2x 微分

微分積分学1 計算問題1000本ノック(を目指して作成中) ※積分の高校レベルとϵ くらいの問題を集めました 大学で学ぶ新しい積分前の練習にお使いください ※まだ全然1000問になるまで道は遠いです 問題を募集中です ※この資料はまだ試作品です 誤りが含まれているかもしれません 発見し · 求函数y=sin(2x^21)的微分, 数学 作业帮用户 举报 用这款APP，检查作业高效又准确！ 扫二维码下载作业帮 拍照搜题，秒出答案，一键查看所有搜题记录 优质解答 y'=cos（2x^21)*(2x^21)' =cos(2x^21)*4x =4xcos(2x^21) 所以微分为： dy=4xcos(2x^21)dx 作业帮用户 举报 其他类似问题 求函数y=2^(sin2t1t2nnnn このように， sin x, cos x, tan x は，すべて tan x2n =t で表される ので， sin x, cos x, tan x を含んだ式 tan x2n =t おとけば， t の積分 となります．（他の方法では不定積分が求められないときでも，この方法で求められます．ただし，他の方法でも求め

If Y Sqrt 1 Cos 2x 1 Cos 2x Find Dy Dx Youtube

1+cos2x 微分

1+cos2x 微分-Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more積分 1/ (cos x )^2 ∫ 1 cos2xdx ∫ 1 cos 2 x d x （ tan x の微分 を参考） = ∫ cos2xsin2x cos2x dx = ∫ cos 2 x sin 2 x cos 2 x d x

正弦函数的积分怎么求 Sin4次方的不定积分怎么求 三人行教育网 Www 3rxing Org

Vor 2 en · こんな検索があったので，回答すっか． $\\int\\frac{1}{1cos^2 x}dx$ 検索されたページは，これとは違う式．cos だの ^2 だのがヒット． 最後のほうに出てくる arctan は高校の教科書にはないが，やっていること自体は，高校の数学IIIの教科積分 1/cos x ∫ 1 cosxdx ∫ 1 cos x d x ∫ 1 cosxdx = ∫ cosx cos2xdx = ∫ cosx 1−sin2x dx ∫ 1 cos x d x = ∫ cos x cos 2 x d x = ∫ cos x 1 − sin 2 x d x f(sinx)cosx f ( sin x) cos x の形に式が変形できたの · cos ²x= (1 cos 2x)/2 所以∫ cos ²xdx=∫1/2dx1/2*∫ cos 2xdx =x/21/4*∫ cos 2xd (2x) =x/21/4*sin2x = (2xsin2x)/4 定积分 就不加常数C了，你把 积分 的上下限代入即可 sin^2 (x)= (1 cos 2x)/2 cos ^2 (x)= (1 cos 2x)/2 cos三次方积分_COS 分之一 三次方积分 weixin_的博

导数 导数应用 极限 积分 积分应用 级数 ode（常微分 方程） 拉普拉斯变换 泰勒/麦克劳林级数 傅立叶级数 函数 直线方程 函数 四则运算和复合 圆锥曲线 矩阵和向量 矩阵 向量 几何 圆锥曲线 三角 恒等式 证明恒等式 三角函数方程 三角不等式 求函数值 化简 反导数计算器 一步步地求反函数 · 最も思いつきやすい方法ですが上の＜重要＞を使った方針2のほうが楽です。 また方針2のほうが \sqrt {1\cos {x}} の積分などに応用するのが簡単なので実はあまりオススメではありません。 答え \displaystyle \int \frac {1} {1\cos {x}} dx=\int \frac {1\cos {x}} {1\cos^2 {x}}dx \\ =\displaystyle \int \frac {dx} {\sin^2 {x}} – \int \frac {\cos {x}} {\sin^2 {x}} dx · を用いて微分していきましょう。 $$y'=(\sin x)'\cos x\sin x(\cos x)'$$ $$=\cos^2 x\sin^2 x$$ $$=\cos 2x$$

Cos^2x 微分, 1/cos^2x 微分, y=cos^2x 微分, y=1/cos^2x 微分, √1cos^2x 微分, log(cos^2x) 微分, sinx/√1cos^2x 微分, sinx/cos^2x 微分, 2sin^2xcos^2x 微分, x/cos^2x 微分, Google その他の · 1/sinx, 1/cosx, 1/tanx の積分の公式と導出方法を解説します。点滴如梦 1年前 已收到3个回答 我来回答 举报 赞 Capricorn星空 幼苗 共回答了18个问题 采纳率：778% 向TA提问 举报

If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

泰勒级数 维基百科 自由的百科全书

覚えておくべき積分公式を整理しました。いずれも積分後の式を微分することで確かめられます。 微分については微分公式一覧（基礎から発展まで）をどうぞ。 目次 基本的な関数の積分公式 一次式の積っぽい積分公式 発展的な三角関数の積分公式 x 2 ± a 2 x^2\pm a^2 x 2 ± a 2 にまつわる積分 · 扩展资料 求函数f (x)的不定积分，就是要求出f (x)的所有的原函数，由原函数的性质可知，只要求出函数f (x)的一个原函数，再加上任意的常数C就得到函数f (x)的不定积分。 全体原函数之间只差任意常数C 证明：如果f (x)在区间I上有原函数，即有一个函数F (x)使对任意x∈I，都有F' (x)=f (x)，那么对任何常数显然也有 F (x)C'=f (x)即对任何常数C，函数F (x)C也是f (x)的 · 逆関数とその微分まとめ \begin{aligned}\sinh ^{1}x&=\log \left(x{\sqrt {x^{2}1}}\right)\\\cosh ^{1}x&=\log \left(x\pm {\sqrt {x^{2}1}}\right)\\\tanh ^{1}x&={\frac {1}{2}}\log {\frac {1x}{1x}}\end{aligned}

If Y Sqrt 1 Cos 2x 1 Cos 2x Find Dy Dx Youtube

3微商与微分 知乎

Cos^2x 微分, cos^2 2x 微分, 1/cos^2x 微分, y=cos^2x 微分, y=1/cos^2x 微分, √1cos^2x 微分, log(cos^2x) 微分, sinx/√1cos^2x 微分, sinx/cos^2x 微分, 2sin^2xcos^2x 微分, Google その他の · 証明1：商の微分公式を使う 証明2：定義に従って計算する 1/tan xの微分 証明1：tan xでできれば1/tan xでもできる 証明2：逆数の微分公式を使う 証明3：平行移動でtanに 証明1：商の微分公式を使う (sin ⁡ x) ′ = cos ⁡ x (\sin x)'=\cos x (sin x) ′ = cos x と (cos ⁡ x) ′ = − sin ⁡对数积分有一个积分的表示法，对所有的正实数 都有定义： 1 在这里，ln表示 自然对数 。 函数1/ln ( t )在 t = 1处有一个 奇点 ，当 x > 1时，这个积分只能用 柯西主值 的概念来解释：

在下列微分方程中 以y C 1 E X C 2 Cos2x C 3 Sin2x C 1 C 2 C 3 为任意常数 为通解的是数学竞赛平台 数学帮 Math110

Matlab微分和导数 Matlab教程

X ⋅ 1 = cosx = cos ⁡ x ①と②で， lim h→0 sinh h lim h → 0 sin ⁡ h h が出現するので，これを考えなければならない必然性が出てきます． つまり微分という単元の前、極限でこれを必ず扱います (詳しくは 三角関数の極限公式とその証明 )． cosx cosHere, if we divide both sides by cos 2x, we get (sin 2x)/(cos 2x) = 2 But the left hand side is the definition for tan 2x Thus, tan 2x = 2 Checking with a calculator, we know that tan 6343 = 2, roughly, so 2x = 6343 This gives x = degreesY= sin −1 x の場合と同様に，合成関数の微分法を使って示してもよい． (3)← y= tan −1 x とは x= tan y (−

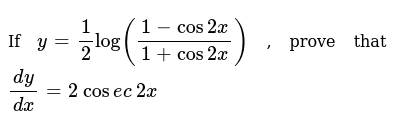
If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

积分公式和常用方法总结 Leemboy的博客 Csdn博客 积分公式

よく使う三角関数関係の公式や積分をこのページにメモしておく。 加法定理 \begin{align} &\sin( \alpha \beta ) = \sin \alpha \cos \beta \cos \alpha \sin \beta \\5pt &\cos ( \alpha \beta ) = \cos \alpha \cos \beta \sin \alpha \sin \beta \end{align} 加法定理は指数関数の性質 \begin{equation*} e^{i(\alpha\beta)} = e^{i\alpha} e^{i\beta} \end$(\sin x)' = \cos x$ を使うと, $(\cos x)' = \sin x$ は, \ (\cos x)' \!=\!0421 · 包括常用： 一、基本导数公式 二、导数的四则运算法则及常用法则 三、高阶导数的运算法则 四、基本初等函数的n阶导数公式 五、微分公式与微分运算法则 六、微分运算法则 七、基本积分公式及常用积分方法 八、补充积分公式 九、常用凑微分公式 十、分部积分法公式 十一、第二换元积分法中的

高等数学上册 微积分 必背公式总结 知乎

Ai攻破高数核心1秒内精确求解微分方程 不定积分 快资讯

微分の公式一覧 このページでは、関数 f (x) f ( x) を 微分 して得られる導関数 f ′(x) f ′ ( x) の基本的な公式を掲載しています。 また、 和や差、積、商の微分公式や合成関数の微分公式なども掲載しています。 導出方法はみなさん自身でご確認の上高校数学から始める微分方程式 フーリエ解析に係る備忘録 Home カレンダー 大学生のための数学教材 Home;22 三角関数の積分 本時の目標 2倍角の公式を用いて， \(\sin^2 x\) や \(\cos^2 x\) などを積分することができる。 「積→和 の公式」を

If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

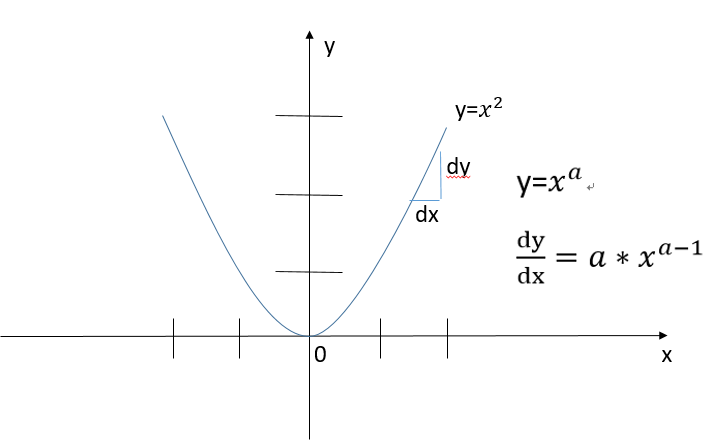
微積分概述 大家一開始在學微積分時應該都是從背公式開始的 首先簡介一下微分 通常老師在介紹時 By Judy Chen Medium

CIVIL BOYHello friends, This is the integral of 1/(a^2cos^2xb^2sin^2x)which is solved by two methods I hope you like this videothis is the most important · x 的积分方法主要有两种：第一种是根据 n n 的奇、偶情况分别采用换元法或者降阶法来求；另一种是递推法。 我们来看换元法和降阶法。 设 n n 是奇数，则我们采用换元法。 例如 ∫ sin5xdx =∫ sin4xsinxdx =∫ (1−cos2x)2(−cosx)′dx =−∫ (1−2cos2xcos4x)d(cosx) =−∫ (1−2u2 u4)du =−(u− 2 3u3 1 u5)C = 2 3cos3x−cosx− 1 5cos5xC ∫ sin 5 ⁡ x d x = ∫ sin 4 ⁡頻出問題 微分積分 不定積分を求める (1cos (2x)) (1 − cos (2x)) ( 1 cos ( 2 x)) 多項式を x x の関数で表現する f (x) = 1 −cos(2x) f ( x) = 1 cos ( 2 x) 関数 F (x) F ( x) は導関数 f (x) f ( x) の不定積分を計算して求めることができます。 Error parsing MathML error on line 1 at column 150 Entity 'int' not defined Error parsing MathML error on line 1 at column 150 Entity 'int' not defined

不定积分的换元积分法 中文数学wiki Fandom

求解微分方程 用seq2seq就够了 性能远超mathematica Matlab 雷锋网

 · ∫(cosx)^2dx=x/2 sin2x /4c。c为积分常数。 过程如下： y=(cosx)^2 =(1cos2x)/2 对其积分： ∫(cosx)^2dx =∫(1cos2x)/2dx = 1/2 ∫（1cos2x）dx微分積分学の分野においては、角度はラジアンを使用する。 微積分において、極限に関する2つの重要な式がある。1つは → =, である。この式ははさみうちの原理から導くことができる。もう1つは以下のTanx的微分等于什么 tanx的微分的推导 ^ (tanx)'= (sinx/cosx)= (sinx)'cosxsinx (cosx)'/ (cosx)^2=1/ (cosx)^2= (secx)^2 因y=arcsinx (1

1

数3の部分積分です なんでcos2xの微分が 1 2sin2xになるのですか Clear

コサイン二乗の微分 コサイン二乗の微分のやり方はサイン二乗の微分と非常に似ています。 やり方その1 合成関数の微分公式を使うと、 $(\cos^2x)'=2\cos x(\cos x)'\\ =2\cos x(\sin x)\\ =2\sin x\cos x$Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history第一步∫sin^2xcos^2x*sinxdx (这部看懂了） 第二步∫（1cos^2x)cos^2x* (d (cosx)) 为什么sinx变成（d (cosx))了?

定积分 0 Pi Sin 3 2x Cos 4 X Dx 求详解 雨露学习互助

单变量微积分笔记12 常微分方程和分离变量 我是8位的 博客园

Sin 2x、cos2x、tan 2xの微分は、合成関数の微分公式を使えば簡単に計算できます。2x=uと置き換えてみると分かりやすいです。 算数から高度な数学まで、網羅的に解説したサイト sin2x、cos2x、tan2xの微分 具体例で学ぶ数学 > 微積分 > sin2x、cos2x、tan2xの微分 最終更新日 $\sin 2x$ の微分は、 $2 · 定积分∫∏0 (xsin^3x)/ (1cos^2x)dx=？ 答案 (π^2)/2π。 过程没法上传。 请读我 更新的博客《定积分∫ (xsin^3x)/ (1cos^2x)dx》 数学 3个回答 · 求下列函数的微分y=sin"(2x1)注：读为sin(2x1)的平方。：dsin(2x1)^2 =2sin(2x1)dsin(2x1 =2s?

Sect 5 5 40 Integral Sin X 1 Cos 2 X Youtube

If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

 · If you mean tex \int \cos^{2} x /tex then you would change it to tex \int \frac{1\cos 2x}{2} /tex Last edited Oct 22, 06 Oct 22, 06 #3 HallsofIvy Science Advisor Homework Helper 41,847 964 And if you mean the general antiderivative of cos(x 2), it is not an "elementary" function That is, it cannot be written in terms of functions you normally learn爱 ^2 =2sin(2x1)dsin(2x1 =2sin(2x1)*cos(2x1)*d(2x1) =2(2x1)cos(2x1)*2dx =2sin(4x2)dx2sinAcosA=sin2A yilwoh 162 73 评论 分享 提交评论 其他答案 ; · dy/dx= （sinx）^2cosx（cosx）^2 カッコを外して微分でも同じ答えがでますが公式的に言えば （f（x）g（x））'=f'（x）g（x）f（x）g'（x） というものを使っています 1cosxの微分はもちろんsinxです 「サイン二乗x」というのをわかりやすくするためにわざわざ答えでは（sinx）^2というふうに書きましたが普段通りsin^2 xというふうに書いていただいて構い

How To Prove Math Dfrac Sqrt 1 Cos 2x 1 Cos 2x Tan X Math Quora

Ai拿下高数一血 求解微分方程 不定积分只需1秒 成绩远超matlab 知乎

 · 1/cos^2θを微分したら何になりますか？1/cos^2θ=1tan^2θ なので、(d/dθ)1/cos^2θ=(d/dθ)(1tan^2θ) =0(d tan^2θ/d tanθ)(d tanθ/dθ) =2tanθ/cos^2θ =2sinθ/cos^3θ

Http Ind Ntou Edu Tw Metex Calculus Secondterm Ch5 singlyintegral 3 Trigonometricfunctionintegral Pdf

導數列表 維基百科 自由的百科全書

1 Cos 2x 微分の仕方教えてください 1 Cos Yahoo 知恵袋

第六节微分及其应用一 微分的概念二 常数和基本初等函数的微分公式与微分运算法则三 微分的应用 Ppt Download

微博搜索

Sin平方x的微分 搜狗搜索

高阶微分方程 Jason S Blog

在下列微分方程中 以y C 1 E X C 2 Cos2x C 3 Sin2x C 1 C 2 C 3 为任意常数 为通解的是数学竞赛平台 数学帮 Math110

Cos2の二乗xは微分すると Sin2乗xですか Tanxの微 Yahoo 知恵袋

实验三用mathematica软件计算导数与微分

Integral Of 1 Cos 2 X Substitution Youtube

换元积分法一 第一类换元积分法二 第二类换元积分法一 第一类换元法例1例1 原因在于被积函数

Q Tbn And9gcrqabt G5qhih R Hl1clj2wbmx732vzgbdz R45o3gs1gbh Usqp Cau

6 6 U4e8c U9636 U5e38 U7cfb U6570 U9f50 U6b21 U7ebf U6027 U5fae U56 U65b9 U7a0b Ppt U7b2c U5341 U4e8c U7ae0 6 6 U5e38 U7cfb U6570 U9f50 U6b21 U7ebf U6027 U5fae U56 U65b9 U7a0b U57fa U672c U601d U8def Course Hero

换元积分和分部积分 U代换积分法常用题型分部积分典型题型

If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

X2cosx2积分

1

6 2一阶线性微分方程 第6章6 2 一阶线性微分方程y P X Y Q X 称为一阶线 Q X 0 Y P X Y 0 微分方程称为一 齐

换元积分法 维基百科 自由的百科全书

一 微分的定义二 微分的几何意义三 微分公式及微分法则四 微分在近似计算中的应用五 小结思考题 Ppt Download

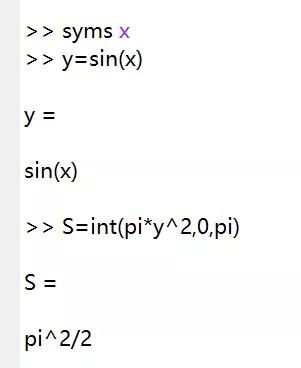
Matlab 不定积分和定积分 知乎

凑微分法技巧19个公式 百度经验

第三章微积分问题的计算机求解微积分问题的解析解函数的级数展开与级数求和问题求解数值微分数值积分问题曲线积分与曲面积分的计算 Ppt Download

求微分方程的通解y Ytanx Sin2x的疑问 雨露学习互助

数据科学中的r和python R语言中的微分运算

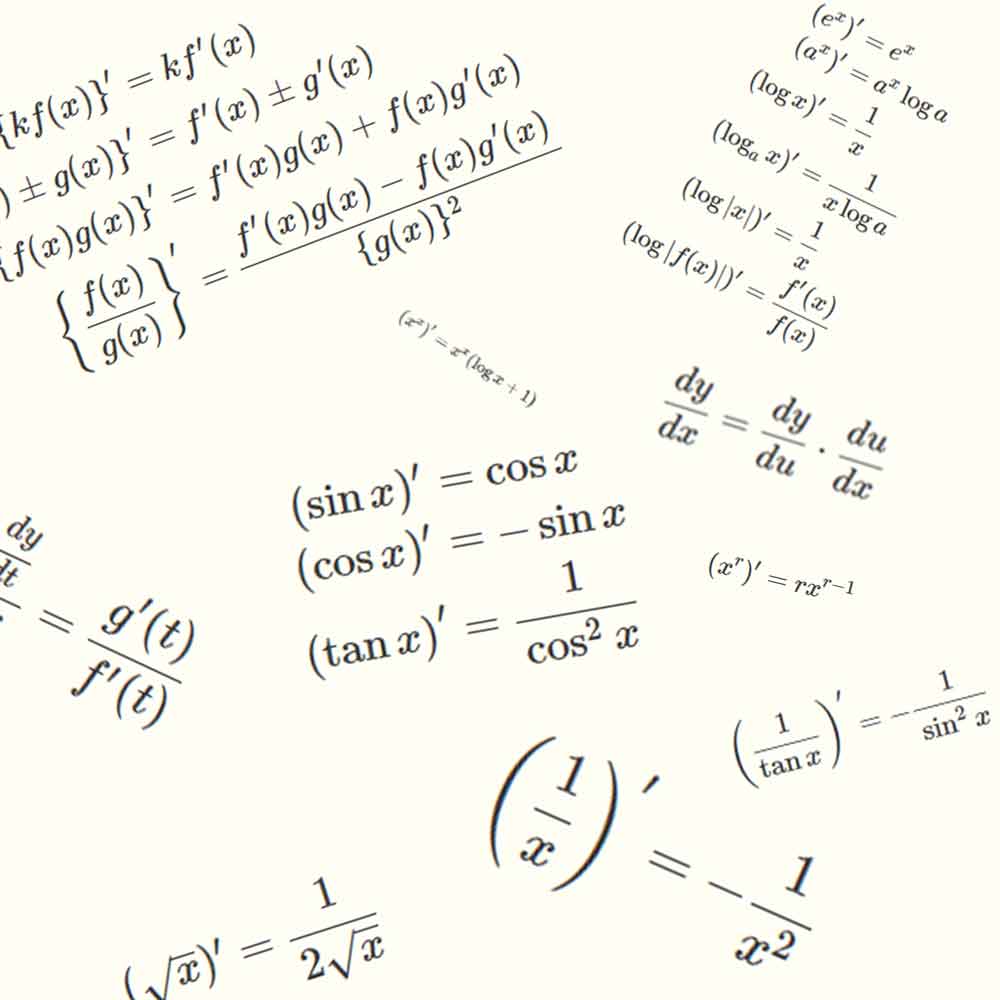
微分の公式一覧

几类三角函数有理式不定积分的求法 科学猫

高校数学 Cos 2x Sin 2xの不定積分 問題編 映像授業のtry It トライイット

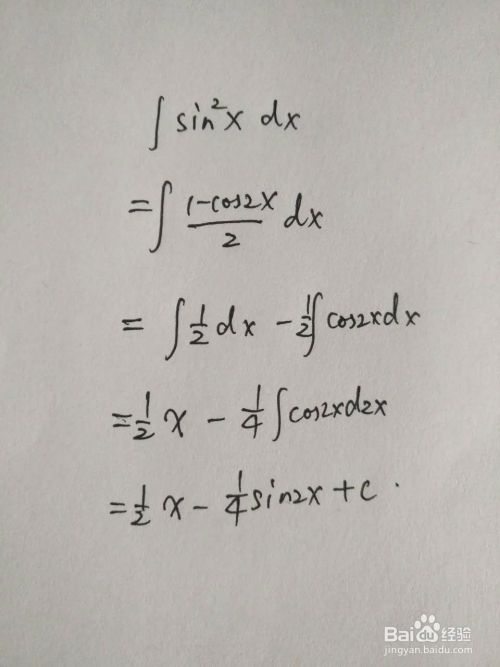
Y Sinx的1 6次方的不定积分 百度经验

Ai攻破高数核心 1秒内精确求解微分方程 不定积分 创事记 新浪科技 新浪网

求微分方程的通解例题 在线图书馆

正弦函数的积分怎么求 Sin4次方的不定积分怎么求 三人行教育网 Www 3rxing Org

高阶微分方程 Jason S Blog

高等数学视频第七十一讲 精选 其他类型的常微分方程 内容包括可直接积分的微分 方程 需要进行变量替换再进行求解的方程 讲解详细 条理清晰 动画演示 通俗易懂 哔哩哔哩

Ai攻破高数核心 1秒内精确求解微分方程 不定积分 性能远超matlab 函数

三角换元法 维基百科 自由的百科全书

Trigonometric Integrals Trigonometric Substitution 三角積分 三角代換積分 Like No Other 藍色愛情海的異想世界 痞客邦

应用对参数的微分法 计算下列积分i S P 2 0 Ln Cos 2 X A 2 Sin 2 X Dx A 0 数学竞赛平台 数学帮 Math110

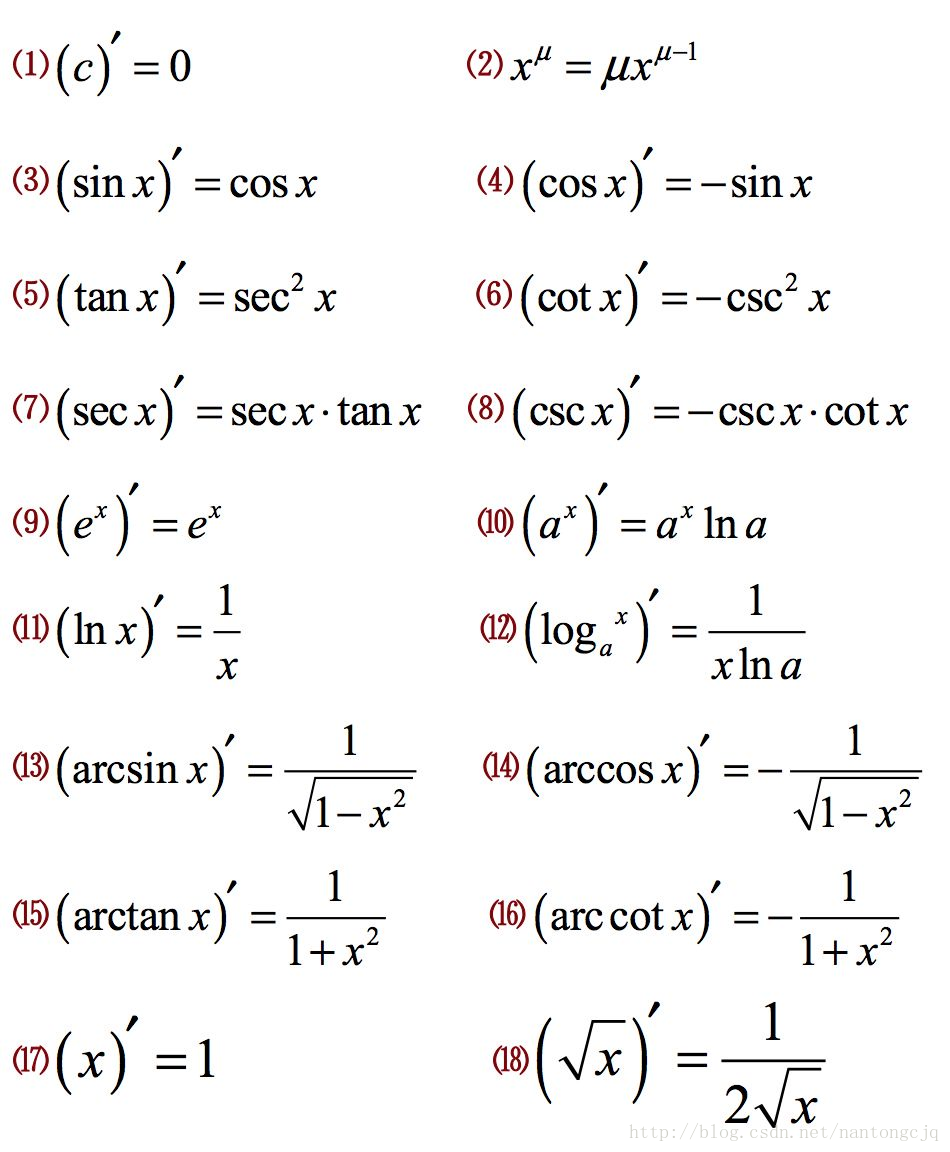
微分 积分 三角函数 数学公式大全 Poem Of Sunshine的专栏 Csdn博客 三角函数微分

If Y 1 2log 1 Cos2x 1 Cos2x Prove That Dy Dx 2 Cos

常用概率数学公式下载 Word模板 爱问共享资料

计算下列导数或微分 求导数或微分 三人行教育网 Www 3rxing Org

三角换元法 维基百科 自由的百科全书

三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ

Integral Of 1 Cos 2 X Substitution Youtube

1 Cos X 1 Sin X 的不定积分推导 90後 小熊大博客 Csdn博客

高等数学 求积分的一些方法 Iv 凑微分法 哔哩哔哩

1 第二节微分 微分概念 微分公式和运算法则 高阶微分 微分在近似计算中的应用举例误差估计 Ppt Download

Cosx 1 Cosxdx 求不定积分 雨露学习互助

剖析17考研数学试题对微分方程的考查 指点18复习 文都考研网

微分方程 单元测试题 三 及参考解答 网易订阅

高阶微分方程 Jason S Blog

Www Cyut Edu Tw Teacher Ft Calculus001 Pdf

2 の1 Cos2xが1になるのはどう言う計算ですか Clear

数学笔记 三角替换1 Sin和cos 我是8位的 Csdn博客

Cos2xdx 万图壁纸网

Y Sinx的1 6次方的不定积分 酷知经验网

Engineering Mathematics 微積分複習

第三章导数与微分社会科学教学部李海霞本章内容 3 1 导数的概念及导数的几何意义 3 2 导数的求导法则 3 3 微分概念及求法 3 4 高阶导数

数3の微分の計算 省略されてる所がどうなっているかわかりません Clear

Sym Py Edu

Cos2xを2回微分したときに 4が出ているのですが Clear

三角関数の微分 公式の証明と例題 高校生向け受験応援メディア 受験のミカタ

实验2 导数 微分 Taylor 公式2 1 实验目的理解导数 微分概念 理解

Alex S Blog 機器如何計算微分 偏微分 上

3

高数微分习题求下列各函数的微分dy 1 Y 3x 2 Ln 1 X 2 Y E X Cosx设由下列方程确定y是x的函 雨露学习互助

第六章单变量微分学

範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X

高数不定积分求 1 2 Cosx Sinx Dx 注 Sinx是在分母上的 不要用万能代换 不要用sinx凑微分 雨露学习互助

Cos Sin 2 積分三角函數的 Kmbymh

42第一类换元积分法1 百度文库

Matlab符号常微分方程求解 有色金属在线

Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube

凑微分法怎么凑 百度经验

三角有理函数及某些无理函数的不定积分 图文 百度文库

17专插本数学复习必看 不定积分精选题目解析 广东专插本教育网

一道数学题 用二阶线性微分方程 求出由电容器 感应器 电阻器构成的闭合电路中的电压及电流 知乎

Integral Of Sin 2x 1 Cos 2 X Substitution Youtube

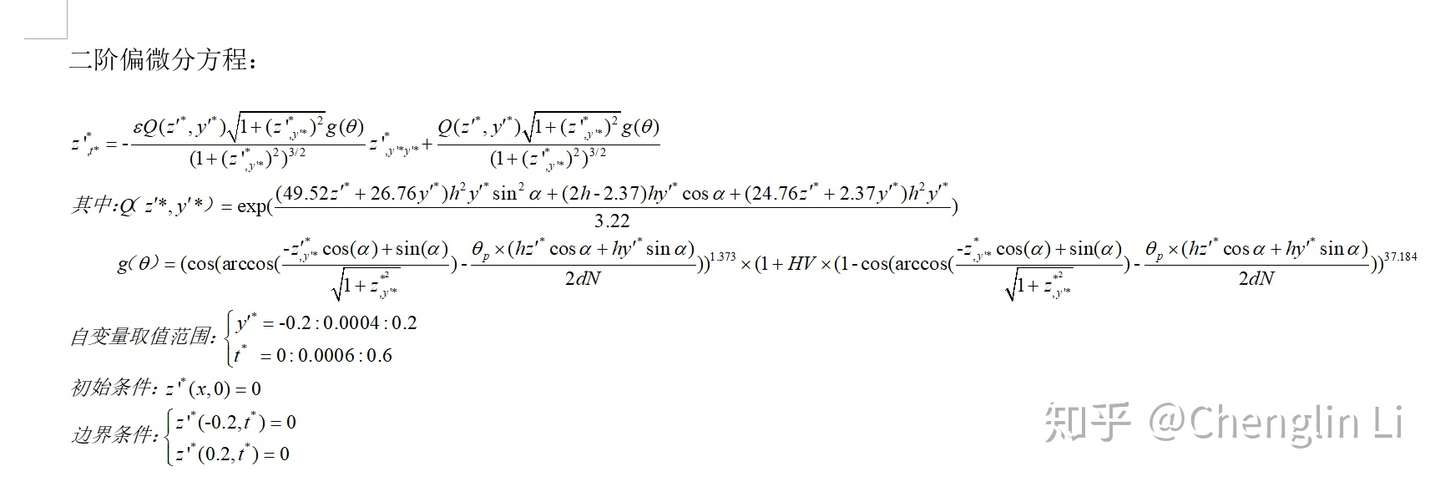
数值计算 五十四 复杂偏微分方程的求解 知乎

2 5函数的微分 早做准备

Incoming Term: 1+cos2x 微分, y=1/cos^2x 微分,